图的最短路径算法
接着坑图论。。。
好久以前就想总结一下了。。。各种最短路233
floyed、dijkstra、bellman、spfa。。。
前提知识
单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前,必须弄清楚最短路径的最优子结构性质。
最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi….Vk..Vs…Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi….Vk..Vs…Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P'(k,s),那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
1、floyed
Floyd算法:
(1)初始时设置一个n阶方阵,令其对角线元素为0,若存在弧<Vi,Vj>,则对应元素为权值;否则为无穷
(2)逐步试着在原直接路径中增加中间顶点,若加入中间点后路径变短,则修改之;否则,维持原值
(3)所有顶点试探完毕,算法结束
伪代码
for k ← 1 to n do
for i ← 1 to n do
for j ← 1 to n do
if (Di,k + Dk,j < Di,j) then
Di,j ← Di,k + Dk,j;
c++核心代码
for(k=1;k<=n;k++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) if(e[i][j]>e[i][k]+e[k][j]) e[i][j]=e[i][k]+e[k][j];
这个算法就是背背代码。。。优点是简单,缺点就是效率太低O(n3)。。。
下面是个板子。。。
#include <stdio.h>
int main()
{
int e[10][10],k,i,j,n,m,t1,t2,t3;
int inf=0x3f3f3f3f; //用inf(infinity的缩写)存储一个我们认为的正无穷值
//读入n和m,n表示顶点个数,m表示边的条数
scanf("%d%d",&n,&m);
//初始化
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
//读入边
//1
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//2
// for(i=1;i<=n;i++)
// for(j=1;j<=m;j++)
// {
// scanf("%d",&e[i][j]);
// if (e[i][j]==0 && i!=j)
// e[i][j]=inf;
// }
//Floyd-Warshall算法核心语句
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(e[i][j]>e[i][k]+e[k][j] )
e[i][j]=e[i][k]+e[k][j];
//输出最终的结果
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
printf("%10d",e[i][j]);
printf("\n");
}
}
2、dijkstra
描述
求单源、无负权的最短路。时效性较好,时间复杂度为O(VV+E),可以用优先队列进行优化,优化后时间复杂度变为0(vlgn)。
源点可达的话,O(VlgV+ElgV)=>O(E*lgV)。
当是稀疏图的情况时,此时E=VV/lgV,所以算法的时间复杂度可为O(V^2) 。可以用优先队列进行优化,优化后时间复杂度变为0(vlgn)。
流程
由前提知识可知,如果存在一条从i到j的最短路径(Vi…..Vk,Vj),Vk是Vj前面的一顶点。那么(Vi…Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根据这种思路,
假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.直到U=V,停止。
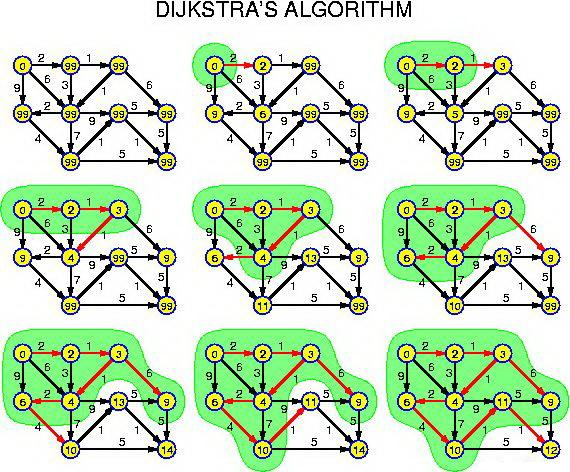
下面是流程图
经典的流程图
动态流程图

详细流程图
(库存的图已经用光了)
(图片均来自于网络)
dij可以用堆优化。。。就是当把点放入最短路径集合的时候,把边压入一个小根堆,更新的时候直接弹出来。。。
伪代码
中文版
int dijkstra(int s,int t) {
初始化S={空集}
d[s] = 0; 其余d值为正无穷大
while (NOT t in S)
{
取出不在S中的最小的d[i];
for (所有不在S中且与i相邻的点j)
if (d[j] > d[i] + cost[i][j]) d[j] = d[i] + cost[i][j];//“松弛”操作”
S = S + {i}; //把i点添加到集合S里
}
return d[t];
}
算导版
DIJKSTRA(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
S ← Ø
Q ← V[G] //V*O(1)
while Q ≠ Ø
do u ← EXTRACT-MIN(Q) //EXTRACT-MIN,V*O(V),V*O(lgV)
S ← S ∪{u}
for each vertex v ∈ Adj[u]
do RELAX(u, v, w) //松弛操作,E*O(1),E*O(lgV)。
实现
先给一个非常详细的,用邻接矩阵实现。。。(效率很低)
来自网络
#include <iostream>
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int map[][5] = { //定义有向图
{0, 10, INT_MAX, INT_MAX, 5},
{INT_MAX, 0, 1, INT_MAX, 2},
{INT_MAX, INT_MAX, 0, 4, INT_MAX},
{7, INT_MAX, 6, 0, INT_MAX},
{INT_MAX, 3, 9, 2, 0}
};
void Dijkstra(
const int numOfVertex, /*节点数目*/
const int startVertex, /*源节点*/
int (map)[][5], /*有向图邻接矩阵*/
int *distance, /*各个节点到达源节点的距离*/
int *prevVertex /*各个节点的前一个节点*/
)
{
vector<bool> isInS; //是否已经在S集合中
isInS.reserve(0);
isInS.assign(numOfVertex, false); //初始化,所有的节点都不在S集合中
/*初始化distance和prevVertex数组*/
for(int i =0; i < numOfVertex; ++i)
{
distance[ i ] = map[ startVertex ][ i ];
if(map[ startVertex ][ i ] < INT_MAX)
prevVertex[ i ] = startVertex;
else
prevVertex[ i ] = -1; //表示还不知道前一个节点是什么
}
prevVertex[ startVertex ] = -1;
/*开始使用贪心思想循环处理不在S集合中的每一个节点*/
isInS[startVertex] = true; //开始节点放入S集合中
int u = startVertex;
for (int i = 1; i < numOfVertex; i ++) //这里循环从1开始是因为开始节点已经存放在S中了,还有numOfVertex-1个节点要处理
{
/*选择distance最小的一个节点*/
int nextVertex = u;
int tempDistance = INT_MAX;
for(int j = 0; j < numOfVertex; ++j)
{
if((isInS[j] == false) && (distance[j] < tempDistance))//寻找不在S集合中的distance最小的节点
{
nextVertex = j;
tempDistance = distance[j];
}
}
isInS[nextVertex] = true;//放入S集合中
u = nextVertex;//下一次寻找的开始节点
/*更新distance*/
for (int j =0; j < numOfVertex; j ++)
{
if (isInS[j] == false && map[u][j] < INT_MAX)
{
int temp = distance[ u ] + map[ u ][ j ];
if (temp < distance[ j ])
{
distance[ j ] = temp;
prevVertex[ j ] = u;
}
}
}
}
}
int main (int argc, const char * argv[])
{
int distance[5];
int preVertex[5];
for (int i =0 ; i < 5; ++i )
{
Dijkstra(5, i, map, distance, preVertex);
for(int j =0; j < 5; ++j)
{
int index = j;
stack<int > trace;
while (preVertex[index] != -1) {
trace.push(preVertex[index]);
index = preVertex[index];
}
cout << "路径:";
while (!trace.empty()) {
cout<<trace.top()<<" -- ";
trace.pop();
}
cout <<j;
cout <<" 距离是:"<<distance[j]<<endl;
}
}
return 0;
}
结果
下面是我写的一个堆优化dij,用的邻接表储存(理论最快)
#include <cstdio>
#include <cstring>
#include <queue>
#define MAXN 10010
using namespace std;
typedef pair<int,int>Pair;
struct node
{
int u,w,v,next;
}e[200010];
int dis[MAXN],st[MAXN];
bool flag[MAXN];
int tot,start,end,n,m,x,y,z;
void add(int x,int y,int z)
{
e[++tot].u=x;
e[tot].v=y;
e[tot].w=z;
e[tot].next=st[x];
st[x]=tot;
}
int dijsktra(int start,int end)
{
memset(dis,127,sizeof dis);
memset(flag,0,sizeof flag);
dis[start]=0;
priority_queue< Pair,vector<Pair>,greater<Pair> >que;
que.push(make_pair(dis[start],start));
while (!que.empty())
{
Pair now=que.top();
que.pop();
if (flag[now.second]) continue;
flag[now.second]=1;
for (int i=st[now.second];i;i=e[i].next)
if (dis[now.second]+e[i].w<dis[e[i].v])
{
dis[e[i].v]=dis[now.second]+e[i].w;
if (!flag[e[i].v]) que.push(make_pair(dis[e[i].v],e[i].v));
}
}
return dis[end];
}
main()
{
scanf("%d%d%d%d",&n,&m,&start,&end);
for (int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);//有向图
}
printf("%d",dijsktra(start,end));
}
例题luogu1139(上面就是题解)
3、Bellman-Ford
简介
Dijkstra算法是处理单源最短路径的有效算法,但它局限于边的权值非负的情况,若图中出现权值为负的边,Dijkstra算法就会失效,求出的最短路径就可能是错的。
这时候,就需要使用其他的算法来求解最短路径,Bellman-Ford算法就是其中最常用的一个。该算法由美国数学家理查德•贝尔曼(Richard Bellman, 动态规划的提出者)和小莱斯特•福特(Lester Ford)发明。
求单源最短路,可以判断有无负权回路(若有,则不存在最短路),时效性较好,时间复杂度O(VE)。
适用条件&范围:
单源最短路径(从源点s到其它所有顶点v);
有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);
边权可正可负(如有负权回路输出错误提示);
差分约束系统;
Bellman-Ford算法的流程如下:
给定图G(V, E)(其中V、E分别为图G的顶点集与边集),源点s,数组Distant[i]记录从源点s到顶点i的路径长度,初始化数组Distant[n]为, Distant[s]为0;
以下操作循环执行至多n-1次,n为顶点数:
对于每一条边e(u, v),如果Distant[u] + w(u, v) < Distant[v],则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值;
若上述操作没有对Distant进行更新,说明最短路径已经查找完毕,或者部分点不可达,跳出循环。否则执行下次循环;
为了检测图中是否存在负环路,即权值之和小于0的环路。对于每一条边e(u, v),如果存在Distant[u] + w(u, v) < Distant[v]的边,则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
可知,Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).
流程
Bellman-Ford算法可以大致分为三个部分
第一,初始化所有点。每一个点保存一个值,表示从原点到达这个点的距离,将原点的值设为0,其它的点的值设为无穷大(表示不可达)。
第二,进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。
第三,遍历途中所有的边(edge(u,v)),判断是否存在这样情况:
d(v) > d (u) + w(u,v)
则返回false,表示途中存在从源点可达的权为负的回路。
之所以需要第三部分的原因,是因为,如果存在从源点可达的权为负的回路。则应为无法收敛而导致不能求出最短路径。
代码
#include<iostream>
#include<cstdio>
using namespace std;
#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点,边,起点
typedef struct Edge //边
{
int u, v;
int cost;
}Edge;
Edge edge[N];
int dis[N], pre[N];
bool Bellman_Ford()
{
for(int i = 1; i <= nodenum; ++i) //初始化
dis[i] = (i == original ? 0 : MAX);
for(int i = 1; i <= nodenum - 1; ++i)
for(int j = 1; j <= edgenum; ++j)
if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛(顺序一定不能反)
{
dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
pre[edge[j].v] = edge[j].u;
}
bool flag = 1; //判断是否含有负权回路
for(int i = 1; i <= edgenum; ++i)
if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
{
flag = 0;
break;
}
return flag;
}
void print_path(int root) //打印最短路的路径(反向)
{
while(root != pre[root]) //前驱
{
printf("%d-->", root);
root = pre[root];
}
if(root == pre[root])
printf("%d\n", root);
}
int main()
{
scanf("%d%d%d", &nodenum, &edgenum, &original);
pre[original] = original;
for(int i = 1; i <= edgenum; ++i)
{
scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);
}
if(Bellman_Ford())
for(int i = 1; i <= nodenum; ++i) //每个点最短路
{
printf("%d\n", dis[i]);
printf("Path:");
print_path(i);
}
else
printf("have negative circle\n");
return 0;
}
结果
这个算法意义不大。。效率太低,根本没法用。但是它的优化spfa还是可以一看的。。。
4、spfa
spfa就是bellman的队列优化。名字叫Shortest Path Faster Algorithm,一听就很有逼格。但是实现非常简单。
简介
SPFA算法可以用于存在负数边权的图,这与dijkstra算法是不同的。
与Dijkstra算法与Bellman-ford算法都不同,SPFA的算法时间效率是不稳定的,即它对于不同的图所需要的时
间有很大的差别。
在最好情形下,每一个节点都只入队一次,则算法实际上变为广度优先遍历,其时间复杂度仅为O(E)。另一方
面,存在这样的例子,使得每一个节点都被入队(V-1)次,此时算法退化为Bellman-ford算法,其时间复杂度为
O(VE)。
SPFA算法在负边权图上可以完全取代Bellman-ford算法,另外在稀疏图中也表现良好。但是在非负边权图中,为了避免最坏情况的出现,通常使用效率更加稳定的Dijkstra算法,以及它的使用堆优化的版本。
流程
几乎所有的最短路算法其步骤都可以分为两步
1.初始化
2.松弛操作
初始化: d数组全部赋值为INF(无穷大);p数组全部赋值为s(即源点),或者赋值为-1,表示还没有知道前驱
然后d[s]=0; 表示源点不用求最短路径,或者说最短路就是0。将源点入队;
(另外记住在整个算法中有顶点入队了要记得标记vis数组,有顶点出队了记得消除那个标记)
队列+松弛操作
读取队头顶点u,并将队头顶点u出队(记得消除标记);将与点u相连的所有点v进行松弛操作,如果能更新估计值(即令d[v]变小),那么就更新,另外,如果点v没有在队列中,那么要将点v入队(记得标记),如果已经在队列中了,那么就不用入队
以此循环,直到队空为止就完成了单源最短路的求解
古老的流程图

首先建立起始点a到其余各点的最短路径表格
首先源点a入队,当队列非空时:
1、队首元素(a)出队,对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点),此时路径表格状态为:

在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点需要入队,此时,队列中新入队了三个结点b,c,d
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点),此时路径表格状态为:

在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要入队,此时队列中的元素为c,d,e
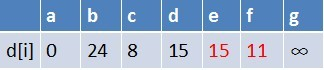
队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点),此时路径表格状态为:
在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。因此e不用入队了,f要入队,此时队列中的元素为d,e,f
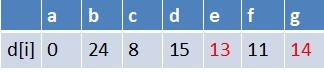
队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:

在最短路径表中,g的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为f,g
队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点),此时路径表格状态为:
在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点),此时路径表格状态为:
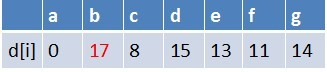
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,此时队列中元素为e,b
队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点),此时路径表格状态为:

在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了
最终a到g的最短路径为14
代码实现
伪代码
ProcedureSPFA; Begin initialize-single-source(G,s); initialize-queue(Q); enqueue(Q,s); while not empty(Q) do begin u:=dequeue(Q); for each v∈adj[u] do begin tmp:=d[v]; relax(u,v); if(tmp<>d[v])and(not v in Q)then enqueue(Q,v); end; end; End;
c++邻接表实现
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
struct node
{
int v,l,next;
}e[20000];
int vis[25100],dis[25100],st[25100];
int en,t,c,s,end,start,x,y,z;
int add(int x,int y,int z)
{
en++;
int i=en;
e[i].l=y;
e[i].v=z;
e[i].next=st[x];
st[x]=i;
}
main()
{
memset(dis,0x3f,sizeof dis);
//memset(st,0,sizeof st);
scanf("%d%d%d%d",&t,&c,&s,&end);
for (int i=1;i<=c;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
start=s;
vis[start]=1;
dis[start]=0;
queue<int>que;
que.push(start);
while (!que.empty())
{
int now=que.front();
que.pop();
int t=st[now];
vis[now]=0;
while (t!=0)
{
if (dis[e[t].l]>dis[now]+e[t].v)
{
dis[e[t].l]=dis[now]+e[t].v;
if (vis[e[t].l]==0)
{
vis[e[t].l]=1;
que.push(e[t].l);
}
}
t=e[t].next;
}
}
printf("%d",dis[end]);
}
例题luogu1139(上面就是题解X2)