图的最大流算法
最近坑了最大流。。。疯狂的图论
最大流真是神奇的算法。。。震惊了我好几次
1.网络流问题(NetWork Flow Problem):
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).
The network flow problem considers a graph G with a set of sources S and sinks T and for which each edge has an assigned capacity (weight), and then asks to find the maximum flow that can be routed from S to T while respecting the given edge capacities.
是不是一脸蒙蔽。。。下面给出一个通俗点的解释
好比你家是汇,自来水厂(有需要的同学可以把自来水厂当成银行之类,以下类似)是源
然后自来水厂和你家之间修了很多条水管子接在一起,水管子规格不一,有的容量大,有的容量小
然后问自来水厂开闸放水,你家收到水的最大流量是多少
如果自来水厂停水了,你家那的流量就是0,当然不是最大的流量,就是零流
但是你给自来水厂交了100w美金,自来水厂拼命水管里通水,但是你家的流量也就那么多不变了,这时就达到了最大流

2.三个基本的性质:
如果 C代表每条边的容量 F代表每条边的流量
一个显然的实事是F小于等于C 不然水管子就爆了
这就是网络流的第一条性质 容量限制(Capacity Constraints):F<x,y> ≤ C<x,y>
再考虑节点任意一个节点 流入量总是等于流出的量 否则就会蓄水(爆炸危险…)或者平白无故多出水(有地下水涌出?)
这是第二条性质 流量守恒(Flow Conservation):Σ F<v,x> = Σ F<x,u>
当然源和汇不用满足流量守恒 我们不用去关心自来水厂的水是河里的 还是江里的
最后一个不是很显然的性质 是斜对称性(Skew Symmetry): F<x,y> = – F<y,x>
这其实是完善的网络流理论不可缺少的 就好比中学物理里用正负数来定义一维的位移一样
百米起点到百米终点的位移是100m的话 那么终点到起点的位移就是-100m
同样的 x向y流了F的流 y就向x流了-F的流
3.容量网络&流量网络&残留网络:
网络就是有源汇的有向图 关于什么就是指边权的含义是什么
容量网络就是关于容量的网络 基本是不改变的(极少数问题需要变动)

流量网络就是关于流量的网络 在求解问题的过程中
通常在不断的改变 但是总是满足上述三个性质
调整到最后就是最大流网络 同时也可以得到最大流值
残留网络往往概括了容量网络和流量网络 是最为常用的
残留网络=容量网络-流量网络
这个等式是始终成立的 残留值当流量值为负时甚至会大于容量值
流量值为什么会为负?有正必有负,记住斜对称性!

4.割&割集:
无向图的割集(Cut Set):C[A,B]是将图G分为A和B两个点集 A和B之间的边的全集
A set of edges of a graph which, if removed (or “cut”), disconnects the graph (i.e., forms a disconnected graph).
网络的割集:C[S,T]是将网络G分为s和t两部分点集 S属于s且T属于t 从S到T的边的全集
带权图的割(Cut)就是割集中边或者有向边的权和
Given a weighted, undirected graph G=(V,E) and a graphical partition of V into two sets A and B, the cut of G with respect to A and B is defined as cut(A,B)=sum_(i in A,j in B)W(i,j),where W(i,j) denotes the weight for the edge connecting vertices i and j. The weight of the cut is the sum of weights of edges crossing the cut.

通俗的理解一下:
割集好比是一个恐怖分子 把你家和自来水厂之间的水管网络砍断了一些
然后自来水厂无论怎么放水 水都只能从水管断口哗哗流走了 你家就停水了
割的大小应该是恐怖分子应该关心的事 毕竟细管子好割一些
而最小割花的力气最小
下面我们来考虑如何求最大流。
首先,假如所有边上的流量都没有超过容量(不大于容量),那么就把这一组流量,或者说,这个流,称为一个可行流。一个最简单的例子就是,零流,即所有的流量都是0的流。 我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。
我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。当找不到增广路的时候,当前的流量就是最大流,这个结论非常重要。
寻找增广路的时候我们可以简单的从源点开始做bfs,并不断修改这条路上的delta量,直到找到源点或者找不到增广路。
这里要先补充一点,在程序实现的时候,我们通常只是用一个c数组来记录容量,而不记录流量,当流量+1的时候,我们可以通过容量-1来实现,以方便程序的实现。
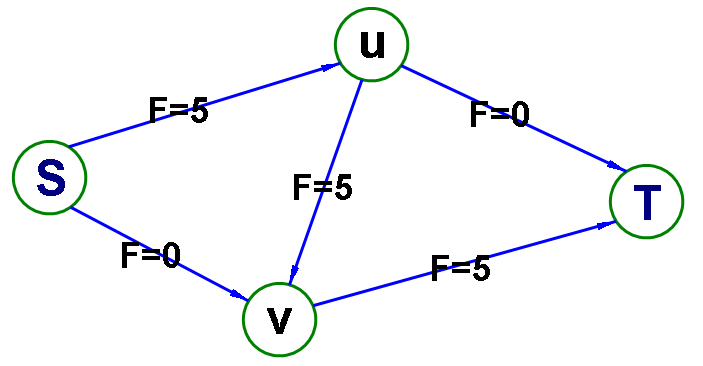
但事实上并没有这么简单,上面所说的增广路还不完整,比如说下面这个网络流模型。
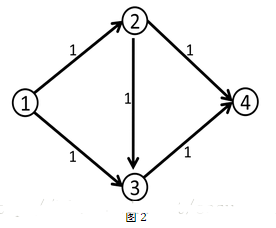
我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个“后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
那么,这么做为什么会是对的呢?我来再通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给“退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会。而这个算法和我刚才算法的代码相比只多了一句话而已。
代码实现
Ford-Fulkerson方法依赖于三种重要思想,这三个思想就是在上文中提到的:残留网络,增广路径和割。
Ford-Fulkerson方法是一种迭代的方法。开始时,对所有的u,v∈V有f(u,v)=0,即初始状态时流的值为0。在每次迭代中,可通过寻找一条“增广路径”来增加流值。增广路径可以看成是从源点s到汇点t之间的一条路径,沿该路径可以压入更多的流,从而增加流的值。反复进行这一过程,直至增广路径都被找出来,根据最大流最小割定理,当不包含增广路径时,f是G中的一个最大流。在算法导论中给出的Ford-Fulkerson实现代码如下:
FORD_FULKERSON(G,s,t)
1 for each edge(u,v)∈E[G]
2 do f[u,v] <— 0
3 f[v,u] <— 0
4 while there exists a path p from s to t in the residual network Gf
5 do cf(p) <— min{ cf(u,v) : (u,v) is in p }
6 for each edge(u,v) in p
7 do f[u,v] <— f[u,v]+cf(p) //对于在增广路径上的正向的边,加上增加的流
8 f[v,u] <— -f[u,v] //对于反向的边,根据反对称性求
第1~3行初始化各条边的流为0,第4~8就是不断在残留网络Gf中寻找增广路径,并沿着增广路径的方向更新流的值,直到找不到增广路径为止。而最后的最大流也就是每次增加的流值cf(p)之和。在实际的实现过程中,我们可以对上述代码做些调整来达到更好的效果。如果我们采用上面的方法,我们就要保存两个数组,一个是每条边的容量数组c,一个就是上面的每条边的流值数组f,在增广路径中判断顶点u到v是否相同时我们必须判断c[u][v]-f[u][v]是否大于0,但是因为在寻找增广路径时是对残留网络进行查找,所以我们可以只保存一个数组c来表示残留网络的每条边的容量就可以了,这样我们在2~3行的初始化时,初始化每条边的残留网络的容量为G的每条边的容量(因为每条边的初始流值为0)。而更新时,改变7~8行的操作,对于在残留网络上的边(u,v)执行c[u][v]-=cf(p),而对其反向的边(v,u)执行c[v][u]+=cf(p)即可。
现在剩下的最关键问题就是如何寻找增广路径。而Ford-Fulkerson方法的运行时间也取决于如何确定第4行中的增广路径。如果选择的方法不好,就有可能每次增加的流非常少,而算法运行时间非常长,甚至无法终止。对增广路径的寻找方法的不同形成了求最大流的不同算法,这也是Ford-Fulkerson被称之为“方法”而不是“算法”的原因。下面将给出Ford-Fulkerson方法的具体实现细节:
int c[MAX][MAX]; //残留网络容量
int pre[MAX]; //保存增广路径上的点的前驱顶点
bool visit[MAX];
int Ford_Fulkerson(int src,int des,int n){ //src:源点 des:汇点 n:顶点个数
int i,_min,total=0;
while(true){
if(!Augmenting_Path(src,des,n))return total; //如果找不到增广路就返回,在具体实现时替换函数名
_min=(1<<30);
i=des;
while(i!=src){ //通过pre数组查找增广路径上的边,求出残留容量的最小值
if(_min>c[pre[i]][i])_min=c[pre[i]][i];
i=pre[i];
}
i=des;
while(i!=src){ //再次遍历,更新增广路径上边的流值
c[pre[i]][i]-=_min;
c[i][pre[i]]+=_min;
i=pre[i];
}
total+=_min; //每次加上更新的值
}
}
Edmonds-Karp算法实际上就是采用广度优先搜索来实现对增广路径的p的计算,代码如下:
bool Edmonds_Karp(int src,int des,int n){
int v,i;
for(i=0;i<n;i++)visit[i]=false;
front=rear=0; //初始化
que[rear++]=src;
visit[src]=true;
while(front!=rear){ //将源点进队后开始广搜的操作
v=que[front++];
//这里如果采用邻接表的链表实现会有更好的效率,但是要注意(u,v)或(v,u)有任何一条
//边存在于原网络流中,那么邻接表中既要包含(u,v)也要包含(v,u)
for(i=0;i<n;i++){
if(!visit[i]&&c[v][i]){ //只有残留容量大于0时才存在边
que[rear++]=i;
visit[i]=true;
pre[i]=v;
if(i==des)return true; //如果已经到达汇点,说明存在增广路径返回true
}
}
}
return false;
}
完整实现
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
int ans[300],g[300][300],m,n,x,y,z;
bool vis[300];
bool bfs(int s,int e)
{
int now;
queue<int>que;
memset(ans,-1,sizeof ans);
memset(vis,0,sizeof vis);
ans[s]=s;
vis[s]=1;
que.push(s);
while(!que.empty())
{
now=que.front();
que.pop();
for (int i=1;i<=n;i++)
if (g[now][i]>0 && !vis[i])
{
vis[i]=1;
ans[i]=now;
if (i==e)
return true;
que.push(i);
}
}
return false;
}
int EdmondsKarp(int s,int e)
{
int flow=0;
while(bfs(s,e))
{
int dis=0x3f3f3f3f;
for (int i=e;i!=s;i=ans[i])
if (dis>g[ans[i]][i])
dis=g[ans[i]][i];
for (int i=e;i!=s;i=ans[i])
{
g[ans[i]][i]-=dis;
g[i][ans[i]]+=dis;
}
flow+=dis;
}
return flow;
}
main()
{
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(g,0,sizeof(g));
for (int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
g[x][y]+=z;
}
printf("%d\n",EdmondsKarp(1,n));
}
}
poj1273 裸的最大流
第二种实现
Dinic 算法
Dinic算法的基本思路:
1、根据残量网络计算层次图。
2、在层次图中使用DFS进行增广直到不存在增广路
3、重复以上步骤直到无法增广
概念
残量网络:包含反向弧的有向图,Dinic要循环的,每次修改过的图都是残量网络,
层次图:分层图,以[从原点到某点的最短距离]分层的图,距离相等的为一层,(比如上图的分层为{1},{2,4},{3})
增广:在现有流量基础上发现新的路径,扩大发现的最大流量(注意:增加量不一定是这条路径的流量,而是新的流量与上次流量之差)
增广路:在现有流量基础上发现的新路径.
剩余流量:当一条边被增广之后(即它是增广路的一部分,或者说增广路通过这条边),这条边还能通过的流量.
反向弧:我们在Dinic算法中,对于一条有向边,我们需要建立另一条反向边(弧),当正向(输入数据)边剩余流量减少I时,反向弧剩余流量增加I
流程:
用BFS建立分层图 注意:分层图是以当前图为基础建立的,所以要重复建立分层图
用DFS的方法寻找一条由源点到汇点的路径,获得这条路径的流量I 根据这条路径修改整个图,将所经之处正向边流量减少I,反向边流量增加I,注意I是非负数
重复步骤2,直到DFS找不到新的路径时,重复步骤1
c++模板题
poj1273 裸的最大流
#include <cstdio>
#include <queue>
#include <cstring>
#define min(x,y) ((x<y)?(x):(y))
using namespace std;
int dis[300],g[300][300],m,n,x,y,z;
int bfs(int s,int e)
{
int now;
queue<int>que;
memset(dis,-1,sizeof dis);
dis[s]=1;
que.push(s);
while(!que.empty())
{
now=que.front();
que.pop();
for (int i=1;i<=n;i++)
if (g[now][i]>0 && dis[i]<0)
{
dis[i]=dis[now]+1;
que.push(i);
}
}
if (dis[e]>0) return 1;
return 0;
}
int finds(int x,int low)
{
int a;
if (x==n) return low;
for (int i=1;i<=n;i++)
if (g[x][i]>0 && dis[x]+1==dis[i] && (a=finds(i,min(low,g[x][i]))))
{
g[x][i]-=a;
g[i][x]+=a;
return a;
}
return 0;
}
int Dinic(int s,int e)
{
int flow=0;
while(bfs(s,e))
{
while(x=finds(s,0x3f3f3f3f))
flow+=x;
}
return flow;
}
main()
{
while(scanf("%d%d",&m,&n)!=EOF)
{
memset(g,0,sizeof(g));
for (int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
g[x][y]+=z;
}
printf("%d\n",Dinic(1,n));
}
}
技巧
- 对于多源多汇问题,只需要添加一个超源点和一个超汇点,将其转化为单源单汇问题即可,如下图。
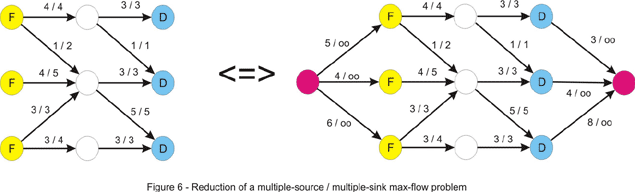
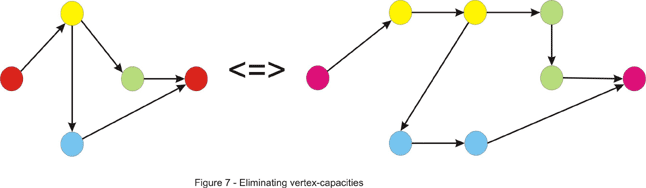
- 对于在顶点处有流量限制的问题,可以对源图进行扩展,既构建一个新的图,新的图的顶点数是源图的两倍,
源图中每个顶点对应新图中的两个顶点,新的顶点之间有一条边相连,边的权值就是源图顶点的权值,如下图。