各种树结构之三 Splay
丧心病狂的splay
伸展树(Splay Tree)是一种二叉排序树,它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。
(1) 伸展树属于二叉查找树,即它具有和二叉查找树一样的性质:假设x为树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
(2) 除了拥有二叉查找树的性质之外,伸展树还具有的一个特点是:当某个节点被访问时,伸展树会通过旋转使该节点成为树根。这样做的好处是,下次要访问该节点时,能够迅速的访问到该节点。
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生,它是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
相比于”二叉查找树“和”AVL树“,学习伸展树时需要重点关注是”伸展树的旋转算法”。
变量声明:f[i]表示i的父结点,ch[i][0]表示i的左儿子,ch[i][1]表示i的右儿子,key[i]表示i的值,cnt[i]表示i结点的关键字出现的次数(bst不允许有重复的节点),size[i]表示包括i的这个子树的大小;sz为整棵树的大小,root为整棵树的根。
int f[Maxn];//father int ch[Maxn][2];//child ; 0 for left ; 1 for right int key[Maxn];//key int cnt[Maxn];//value int siz[Maxn];//size of subtree int sz,root;//size of tree and root
还有几个基本操作:
【clear操作】:将当前点的各项值都清0(用于删除之后)
//clear the ndoe
void clear(int x)
{
ch[x][0]=ch[x][1]=f[x]=cnt[x]=key[x]=siz[x]=0;
}
【getson操作】:判断当前点是它父结点的左儿子还是右儿子
//rightson return 1;left son return 0
int getson(int x)
{
return ch[f[x]][1]==x;
}
【update操作】:更新当前点的size值(用于发生修改之后)
//update the size
void update(int x)
{
siz[x]=cnt[x];
if (ch[x][0]) siz[x]+=siz[ch[x][0]];
if (ch[x][1]) siz[x]+=siz[ch[x][1]];
}
【rotate操作】
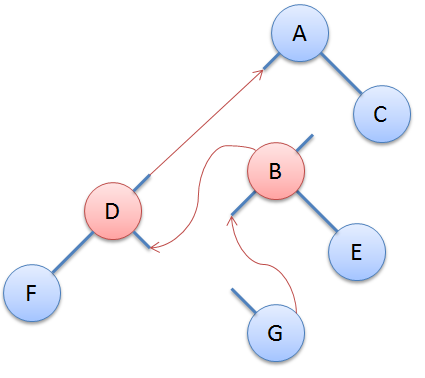
比如我们现在有一棵splay
我们要把D旋转到他父亲的位置
我们先找到三条必须断掉的边
然后对于D,B>D,所以B要成为D的右孩子,但是已经有G了。因为G<B,所以正好连到B的左孩子,最后把A和D连起来
然后就完成了
具体步骤
step 1:
找出D的父亲结点(B)以及父亲的父亲(A)并记录。判断D是B的左结点还是右结点,设为K。
step 2:
将D与K关系相反的儿子的父亲,记为B与K关系相同的儿子(这里即为D的右儿子的父亲记为B的左儿子);
将D与K关系相反的儿子的父亲记为B(这里即为把G的父亲记为B);
将B的父亲即为D;将D与K关系相反的儿子记为B(这里即为把D的右儿子记为B);
将D的父亲记为A,A的儿子记为D。
step 3:
update一下当前点和各个父结点的各个值
代码
//retation
int rotate(int x)
{
int fa=f[x],fafa=f[fa],k=getson(x);
ch[fa][k]=ch[x][k^1];f[ch[fa][k]]=fa;
ch[x][k^1]=fa;f[fa]=x;
f[x]=fafa;
if (fafa)
ch[fafa][ch[fafa][1]==fa]=x;
update(fa);update(x);
}
【splay操作】
伸展操作只是在不停的rotate,一直到达到根。
splay的过程中需要分类讨论,如果是三点一线的话(x,x的父亲,x的祖父)需要先rotate x的父亲,否则需要先rotate x本身(否则会形成单旋使平衡树失衡)
//rotate until x is the root
void splay(int x)
{
for (int fa;fa=f[x];rotate(x))
if (f[fa])
rotate(getson(x)==getson(fa) ? fa : x);
root=x;
}
【insert操作】
其实插入操作是比较简单的,和普通的bst基本一样。
step 1:
如果root=0,即树为空的话,新建一个节点,直接返回即可。
step 2:
按照二叉查找树的方法一直向下找,其中:
如果遇到一个结点的关键字等于当前要插入的点的话,我们就等于把这个结点加了一个cnt。因为在bst中是不可能出现两个相同的点的。并且要将当前点和它父亲结点的各项值更新一下。做一下splay。
如果已经到了最底下了,那么就可以直接插入。整个树的大小要+1,新结点的左儿子右儿子(虽然是空)父亲还有各项值要一一对应。并且最后要做一下他父亲的update(做他自己的没有必要)。做一下splay。
//ceate a new splay node
void create(int v)
{
sz++;
ch[sz][0]=ch[sz][1]=f[sz]=0;
key[sz]=v;
cnt[sz]=1;
siz[sz]=1;
//root=sz;
}
//insert a node
void insert(int v)
{
if (!root)
create(v),root=sz;
else
{
int now=root,fa=0;
while(1)
{
if (key[now]==v)
{
cnt[now]++;
update(now);update(fa);
splay(now);
break;
}
fa=now;
now=ch[fa][v>key[fa]];
if (!now)
{
create(v);
f[sz]=fa;
ch[fa][v>key[fa]]=sz;
update(fa);
splay(sz);
break;
}
}
}
}
【findpos操作】查询x的排名
初始化:ans=0,当前点=root
和其它二叉搜索树的操作基本一样。但是区别是:
如果x比当前结点小,即应该向左子树寻找,ans不用改变。
如果x比当前结点大,即应该向右子树寻找,ans需要加上左子树的大小以及根的大小(这里的大小指的是权值)。
不要忘记了再splay一下。
//find x's pos
int findpos(int v)
{
int now=root,ans=0;
while(1)
{
if (v<key[now])
now=ch[now][0];
else
{
ans+=ch[now][0]?siz[ch[now][0]]:0;
if (v==key[now])
{
splay(now);
return ans+1;
}
ans+=cnt[now];
now=ch[now][1];
}
}
}
【findx操作】找到排名为x的点
初始化:当前点=root
和上面的思路基本相同:
如果当前点有左子树,并且x比左子树的大小小的话,即向左子树寻找;
否则,向右子树寻找:先判断是否有右子树,然后记录右子树的大小以及当前点的大小(都为权值),用于判断是否需要继续向右子树寻找。
//find pos's x
int findx(int x)
{
int now=root;
while(1)
{
if (ch[now][0] && x<=siz[ch[now][0]])
now=ch[now][0];
else
{
int temp=(ch[now][0]?siz[ch[now][0]]:0)+cnt[now];
if (x<=temp)
return key[now];
x-=temp;
now=ch[now][1];
}
}
}
【求x的前驱(后继),前驱(后继)定义为小于(大于)x,且最大(最小)的数】
这类问题可以转化为将x插入,求出树上的pre(nex),再将x删除的问题。
【pre/nex操作】
这个操作十分的简单,只需要理解一点:在我们做insert操作之后做了一遍splay。这就意味着我们把x已经splay到根了。求x的前驱其实就是求x的左子树的最右边的一个结点,后继是求x的右子树的左边一个结点。
int pre()
{
int now=ch[root][0];
while(ch[now][1])
now=ch[now][1];
return now;
}
int nex()
{
int now=ch[root][1];
while(ch[now][0])
now=ch[now][0];
return now;
}
【del操作】
删除操作是最后一个稍微有点麻烦的操作。
step 1:findpos一下x。目的是:将x旋转到根。
step 2:那么现在x就是根了。如果cnt[root]>1,即不只有一个x的话,直接-1返回。
step 3:如果root并没有孩子,就说名树上只有一个x而已,直接clear返回。
step 4:如果root只有左儿子或者右儿子,那么直接clear root,然后把唯一的儿子当作根就可以了(f赋0,root赋为唯一的儿子)
剩下的就是它有两个儿子的情况。
step 5:我们找到新根,也就是x的前驱(x左子树最大的一个点),将它旋转到根。然后将原来x的右子树接到新根的右子树上(注意这个操作需要改变父子关系)。这实际上就把x删除了。不要忘了update新根。
代码
void del(int x)
{
int t=findpos(x);
if (cnt[root]>1)
{
cnt[root]--;
update(root);
return;
}
//none
if (!ch[root][0] && !ch[root][1])
{
clear(root);
root=0;
return;
}
//one
if (!ch[root][1])
{
int temp=root;
root=ch[root][0];
f[root]=0;
clear(temp);
return;
}
else
if (!ch[root][0])
{
int temp=root;
root=ch[root][1];
f[root]=0;
clear(temp);
return;
}
//two
int pre1=pre(),temp=root;
splay(pre1);
f[ch[temp][1]]=root;
ch[root][1]=ch[temp][1];
clear(temp);
update(root);
}
操作均来源于bzoj3224
总代吗
#include <cstdio>
#include <cstdlib>
#define Maxn 500000
using namespace std;
int f[Maxn],ch[Maxn][2],siz[Maxn],key[Maxn],sz,root;
int get(int x){return ch[f[x]][1]==x;}
void update(int x){siz[x]=siz[ch[x][1]]+siz[ch[x][0]];}
void clear(int x){f[x]=ch[x][0]=ch[x][1]=siz[x]=key[x]=0;}
void create(int v){sz++;ch[sz][0]=ch[sz][1]=f[sz]=0;siz[sz]=1;key[sz]=v;}
void rot(int x)
{
int k=get(x),fa=f[x],fafa=f[fa];
ch[fa][k]=ch[x][!k];f[ch[x][!k]]=fa;
ch[x][!k]=fa;f[fa]=x;
f[x]=fafa;
if (fafa)
ch[fafa][ch[fafa][1]==fa]=x;
update(fa);update(x);
}
void splay(int x)
{
for (int fa;fa=f[x];rot(x))
if (f[fa])
rot(get(x)==get(fa)?fa:x);
root=x;
}
void insert(int v)
{
if (!root)
{create(v);root=sz;return;}
int now=root,fa=0;
while(1)
{
fa=now;now=ch[now][key[now]<v];
if (!now)
{create(v);f[sz]=fa;ch[fa][key[fa]<v]=sz;update(fa);splay(sz);return;}
}
}
void del(int v)
{
int now=root,fa=0;
while(1){if (key[now]==v){splay(now);break;}now=ch[now][key[now]<v];}
if (!ch[root][1] && !ch[root][0])
clear(root),root=0;
else if (!ch[root][1] || !ch[root][0])
{
int x=ch[root][1]?ch[root][1]:ch[root][0];
clear(root);f[x]=0,root=x;
}
else
{
int pre=ch[root][0],oldr=root;
while (ch[pre][1]) pre=ch[pre][1];
splay(pre);
ch[root][1]=ch[oldr][1];
f[ch[oldr][1]]=root;
clear(oldr);
update(root);
}
}
//preparation is over
//write your legendary
main()
{
}
The end.